BLOQUE 1: Problemas aritméticos y algebraicos
Números positivos y su representación
Conversión de fracciones
Jerarquía (orden) de las operaciones numéricas
Números reales
Variables y expresiones algebraicas
Autoevaluación para el bloque 1
Números positivos y su representación
Conversión de fracciones
Jerarquía (orden) de las operaciones numéricas
Números reales
Variables y expresiones algebraicas
Autoevaluación para el bloque 1
BLOQUE 2: Congruencia de triángulos
Representación de los números reales y operaciones Autoevaluación para el bloque 2
Representación de los números reales y operaciones Autoevaluación para el bloque 2
BLOQUE 3: Sumas y sucesiones de números
Sucesiones y series aritméticas
Sucesiones y series geométricas
Autoevaluación para el bloque 3
Sucesiones y series aritméticas
Sucesiones y series geométricas
Autoevaluación para el bloque 3
BLOQUE 4: Transformaciones algebraicas I
Conceptos básicos
Operaciones con polinomios
Productos notables
Factorización
Autoevaluación para el bloque 4
Conceptos básicos
Operaciones con polinomios
Productos notables
Factorización
Autoevaluación para el bloque 4
BLOQUE 5: Transformaciones algebraicas II
Factorización de trinomios de la forma + bx + c
Factorización de trinomios de la forma ax2 + bx + c
Factorización de polinomios que requieren combinar técnicas
Simplificación de fracciones racionales (fracciones algebraicas)
División de polinomios
Autoevaluación para el bloque 5
Factorización de trinomios de la forma + bx + c
Factorización de trinomios de la forma ax2 + bx + c
Factorización de polinomios que requieren combinar técnicas
Simplificación de fracciones racionales (fracciones algebraicas)
División de polinomios
Autoevaluación para el bloque 5
BLOQUE 6: Ecuaciones lineales I
Modelado y análisis de ecuaciones lineales
Ecuaciones equivalentes
Técnicas para resolver ecuaciones lineales
Ecuaciones lineales con coeficientes fraccionarios
Sistema coordenado en el plano
Relación entre funciones y ecuaciones lineales
Autoevaluación para el bloque 6
Modelado y análisis de ecuaciones lineales
Ecuaciones equivalentes
Técnicas para resolver ecuaciones lineales
Ecuaciones lineales con coeficientes fraccionarios
Sistema coordenado en el plano
Relación entre funciones y ecuaciones lineales
Autoevaluación para el bloque 6
BLOQUE 7: Ecuaciones lineales II
Solución gráfica de un sistema lineal de dos ecuaciones con dos incógnitas
Técnicas analíticas para la de sistemas de dos ecuaciones con dos incógnitas
Autoevaluación para el bloque 7
Solución gráfica de un sistema lineal de dos ecuaciones con dos incógnitas
Técnicas analíticas para la de sistemas de dos ecuaciones con dos incógnitas
Autoevaluación para el bloque 7
BLOQUE 8: Ecuaciones lineales III
Resolución de un sistema lineal de tres ecuaciones con tres incógnitas por sustitución
Resolución de un sistema lineal de tres ecuaciones con tres incógnitas por determinantes 193 Autoevaluación para el bloque 8
Resolución de un sistema lineal de tres ecuaciones con tres incógnitas por sustitución
Resolución de un sistema lineal de tres ecuaciones con tres incógnitas por determinantes 193 Autoevaluación para el bloque 8
BLOQUE 9: Ecuaciones cuadráticas I
Identificación de ecuaciones cuadráticas
Resolución de una ecuación cuadrática completando el trinomio cuadrado perfecto
Resolución de ecuaciones cuadráticas con raíces complejas
Estructura de una ecuación cuadrática a partir de soluciones reales y complejas
Autoevaluación para el bloque 9
Identificación de ecuaciones cuadráticas
Resolución de una ecuación cuadrática completando el trinomio cuadrado perfecto
Resolución de ecuaciones cuadráticas con raíces complejas
Estructura de una ecuación cuadrática a partir de soluciones reales y complejas
Autoevaluación para el bloque 9
BLOQUE 10: Ecuaciones cuadráticas II
Relación entre la función y la ecuación cuadráticas
Efecto del parámetro a en el ancho y la concavidad de la parábola
Forma estándar de la función cuadrática
Raíces de la ecuación cuadrática ax2 + bx + c = 0
Interpretación de la fórmula cuadrática
Autoevaluación para el bloque 9
Registro de avance y aprovechamiento
Fórmulas matemáticas
Matemáticas II de JimenezRelación entre la función y la ecuación cuadráticas
Efecto del parámetro a en el ancho y la concavidad de la parábola
Forma estándar de la función cuadrática
Raíces de la ecuación cuadrática ax2 + bx + c = 0
Interpretación de la fórmula cuadrática
Autoevaluación para el bloque 9
Registro de avance y aprovechamiento
Fórmulas matemáticas
BLOQUE 2: Congruencia de triángulos
Congruencia de triángulos
Más propiedades de los triángulos
Congruencia de triángulos
Más propiedades de los triángulos
BLOQUE 3: Semejanza de triángulos
Semejanza de triángulos
Teorema de Tales
Teorema de Pitágoras
Semejanza de triángulos
Teorema de Tales
Teorema de Pitágoras
BLOQUE 4: Propiedades de los polígonos
Polígonos. Definición
Clasificación de los polígonos
Elementos de un polígono
Propiedades de los polígonos
Perímetro y área de un polígono
Cuadriláteros
Perímetros y áreas
Polígonos. Definición
Clasificación de los polígonos
Elementos de un polígono
Propiedades de los polígonos
Perímetro y área de un polígono
Cuadriláteros
Perímetros y áreas
BLOQUE 5: La circunferencia
Definición y propiedades de la circunferencia
Propiedades de los ángulos en la circunferencia
Perpendiculares a las cuerdas
Tangentes a los círculos
Perímetro y área de un círculo
Definición y propiedades de la circunferencia
Propiedades de los ángulos en la circunferencia
Perpendiculares a las cuerdas
Tangentes a los círculos
Perímetro y área de un círculo
BLOQUE 6: Funciones trigonométricas de triángulos rectángulos
Sistemas de unidades para medir ángulos
Definición de trigonometría
Definición de las funciones trigonométricas
Funciones trigonométricas recíprocas
Valores naturales de las funciones trigonométricas
Funciones trigonométricas de los ángulos de 30°, 45° y 60°
Resolución de triángulos rectángulos
Sistemas de unidades para medir ángulos
Definición de trigonometría
Definición de las funciones trigonométricas
Funciones trigonométricas recíprocas
Valores naturales de las funciones trigonométricas
Funciones trigonométricas de los ángulos de 30°, 45° y 60°
Resolución de triángulos rectángulos
BLOQUE 7: Aplicación de las funciones trigonométricas
Ángulos de cualquier magnitud
Angulo de referencia para ángulos situados en los diferentes cuadrantes
Definición de las funciones trigonométricas en las coordenadas cartesianas
Circulo unitario. Funciones trigonométricas representadas por un segmento
Identidades trigonométricas recíprocas y pitagóricas
Gráficas de las funciones seno, coseno y tangente
Ángulos de cualquier magnitud
Angulo de referencia para ángulos situados en los diferentes cuadrantes
Definición de las funciones trigonométricas en las coordenadas cartesianas
Circulo unitario. Funciones trigonométricas representadas por un segmento
Identidades trigonométricas recíprocas y pitagóricas
Gráficas de las funciones seno, coseno y tangente
BLOQUE 8: Leyes de senos y cosenos
Leyes de senos y cosenos
Leyes de senos y cosenos
BLOQUE 9: Estadística elemental
¿Para qué sirve la estadística?
Definiciones básicas
Distribución de frecuencias
Marca de clase
Histograma
Polígono de frecuencias
Medidas de tendencia central
Medidas de variación o de dispersión
Rango
Desviación estándar
Varianza
Desviación estándar para datos agrupados
¿Para qué sirve la estadística?
Definiciones básicas
Distribución de frecuencias
Marca de clase
Histograma
Polígono de frecuencias
Medidas de tendencia central
Medidas de variación o de dispersión
Rango
Desviación estándar
Varianza
Desviación estándar para datos agrupados
BLOQUE 10: Conceptos elementales de probabilidad
Elementos de probabilidad
Eventos deterministas y aleatorios
Espacio muestral
Eventos
Definición de probabilidad
Enfoques de la probabilidad
Leyes de probabilidad
Registro personal de avance y aprovechamiento
Autoevaluación para el bloque 1
Autoevaluación para el bloque 2
Autoevaluación para el bloque 3
Autoevaluación para el bloque 4
Autoevaluación para el bloque 5
Autoevaluación para el bloque 6
Autoevaluación para el bloque 7
Autoevaluación para el bloque 8
Autoevaluación para el bloque 9
Autoevaluación para el bloque 10
Fórmulas matemáticas
Álgebra
Geometría básica
Trigonometría
Índice analítico
Matemáticas III de JimenezElementos de probabilidad
Eventos deterministas y aleatorios
Espacio muestral
Eventos
Definición de probabilidad
Enfoques de la probabilidad
Leyes de probabilidad
Registro personal de avance y aprovechamiento
Autoevaluación para el bloque 1
Autoevaluación para el bloque 2
Autoevaluación para el bloque 3
Autoevaluación para el bloque 4
Autoevaluación para el bloque 5
Autoevaluación para el bloque 6
Autoevaluación para el bloque 7
Autoevaluación para el bloque 8
Autoevaluación para el bloque 9
Autoevaluación para el bloque 10
Fórmulas matemáticas
Álgebra
Geometría básica
Trigonometría
Índice analítico
BLOQUE 1. Lugares geométricos
BLOQUE 2. Segmentos rectilíneos y polígonos
BLOQUE 3. La recta
BLOQUE 4. Formas de la ecuación de la recta
BLOQUE 5. Ecuación de la circunferencia con centro en el origen
BLOQUE 6. Ecuación de la circunferencia con centro fuera del origen
BLOQUE 7. Ecuación de la parábola con vértice en el origen
BLOQUE 8. Ecuación de la parábola con vértice fuera del origen
BLOQUE 9. Ecuación de la elipse con centro en el origen
BLOQUE 10. Ecuación de la elipse con centro fuera del origen
BLOQUE 2. Segmentos rectilíneos y polígonos
BLOQUE 3. La recta
BLOQUE 4. Formas de la ecuación de la recta
BLOQUE 5. Ecuación de la circunferencia con centro en el origen
BLOQUE 6. Ecuación de la circunferencia con centro fuera del origen
BLOQUE 7. Ecuación de la parábola con vértice en el origen
BLOQUE 8. Ecuación de la parábola con vértice fuera del origen
BLOQUE 9. Ecuación de la elipse con centro en el origen
BLOQUE 10. Ecuación de la elipse con centro fuera del origen
Cálculo Integral de Jimenez
Unidad 1. Diferenciales e integral indefinida
Unidad 2. Integral definida y métodos de integración
Unidad 3. Teorema fundamental del cálculo
Unidad 4. Más técnicas de integración
Fórmulas matemáticas
Descarga
Geometría Analítica de Jimenez
UNIDAD 1: SISTEMA COORDENADO LINEAL Y GRÁFICAS DE UNA ECUACIÓN
Sistema coordenado lineal
Sistema coordenado en el plano
Distancia entre dos puntos en el plano
División de un segmento entre una razón dada
Ángulo de inclinación y pendiente de una recta
Paralelismo y perpendicularidad
Gráficas de una ecuación
Representación gráfica de las ecuaciones
Intersecciones de una gráfica
Simetría
UNIDAD 2: LA LÍNEA RECTA
Línea recia
Ecuación de la recta que pasa por un punto y tiene una pendiente dada
Ecuación de la recta dadas su pendiente y la ordenada en el origen
Ecuación de la recta en su forma simétrica
Forma general de la ecuación de la recta
Ecuación general de primer grado
Rectas notables de un triángulo
Forma normal de la ecuación de la recta
Distancia de un punto a una recta
UNIDAD 3: LA CIRCUNFERENCIA
UNIDAD 4: LA PARÁBOLA
UNIDAD 5: CÓNICAS Y ECUACIONES DE SEGUNDO GRADO
Descarga
Álgebra I de Armando Rojo

Contenido:
Capítulo 1: Nociones de lógica.
Capítulo 2: Conjuntos.
Capítulo 3: Relaciones
Capítulo 4: Funciones.
Capítulo 5: Leyes de composición.
Capítulo 6: Coordinabilidad. Inducción completa. Combinatoria.
Capítulo 7: Sistemas axiomáticos.
Capítulo 8: Estructura de grupo
Capítulo 9: Estructuras de anillo y de cuerpo. Enteros y racionales.
Capítulo 10: Números reales.
Capítulo 11: El cuerpo de los números complejos.
Descargar
Matemáticas Discreta y Combinatoria, Ralph P. Grimaldi + Solucionario
PARTE 1. 1. Principios fundamentales de Conteo. Las Reglas de Suma y Producto. Permutaciones. Combinaciones: El teorema binomial. Combinaciones con repetición. El Consejo Catalán de Números de Internet (opcional). Resumen y revisión histórica. 2. Fundamentos de la Lógica. Conectivos básicos y Tablas de Verdad. Equivalencia lógica: las leyes de la lógica. Implicación lógica: Reglas de Inferencia. El uso de los cuantificadores. Cuantificadores, Definiciones, y pruebas de los Teoremas. Resumen y revisión histórica. 3. Teoría de conjuntos. Conjuntos y subconjuntos. Conjunto de Operaciones y las leyes de teoría de conjuntos. Conteo y diagramas de Venn. Una primera palabra en Probabilidad. Los axiomas de la Probabilidad (Opcional). Probabilidad condicionada: Independencia (Opcional). Variables aleatorias discretas (Opcional). Resumen y revisión histórica. 4. Propiedades de los enteros: Inducción Matemática. The Well-Pedidos Principio: Inducción Matemática. Definiciones recursivas. La División Algoritmo: números primos. El máximo común divisor: El algoritmo de Euclides. El teorema fundamental de la Aritmética. Resumeny revisión histórica. 5. Relaciones y funciones. Productos y Relaciones cartesiano. Funciones: Normal y uno a uno. En funciones: Números de Stirling del segundo tipo. Funciones especiales. El casillero principio. Función Composición y funciones inversas. Complejidad. Análisis de algoritmos. Resumen y revisión histórica. 6. Idiomas: Las máquinas de estados finitos. Idioma: El Conjunto de Teoría de Cuerdas. Las máquinas de estados finitos: un primer encuentro. Las máquinas de estados finitos: Un Segundo Encuentro. Resumen y revisión histórica. 7. Relaciones: La segunda vez. Relaciones Revisited: Propiedades de las relaciones. Reconocimiento equipo: Cero Uno Matrices y Dirigido Gráficos. Órdenes parciales: Diagramas de Hasse. Relaciones de equivalencia y particiones. Las máquinas de estados finitos: la reducción al mínimo del proceso. Resumen y revisión histórica.
PARTE 2. 8. El principio de inclusión y exclusión. El principio de inclusión y exclusión. Generalización del principio. Derangements: no hay nada en su lugar. Torre Polinomios. Acuerdos con posiciones Prohibida. Resumen y revisión histórica. 9. Funciones generadoras. Ejemplos de introducción. Definición y ejemplos: Calculational Técnicas. Particiones de enteros. La Generación de Funciones exponencial. La suma del operador.Resumen y revisión histórica. 10. Relaciones de recurrencia. La primera Orden Recurrencia relación lineal. El segundo orden lineal Recurrencia Homogénea relación con coeficientes constantes. La recurrencia Nonhomogeneous relación. El Método de Generación de funciones. Un tipo especial de relación no lineal de recurrencia (Opcional). Algoritmos divide y vencerás. Resumen y revisión histórica.

En el capítulo I se presenta las matrices que son utilizados en la resolución de sistemas de ecuaciones lineales, además su utilidad mayor en este campo es en la presentación de árboles y grafos que se hace mediante matrices.
En el Capítulo II presenta Álgebra de Boole que permite presentar funciones con dos estados.
En el Capítulo III se presenta Mapas de Karnaugh que permiten simplificar las funciones algebraicas.
En el Capítulo IV Se tiene las técnicas de conteo las variaciones, permutaciones y combinaciones las cuales son parte de las Matemáticas Discretas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
En el Capítulo V y en el Capítulo VI se presenta la teoría de grafos, árboles y sus aplicaciones, para nadie es novedad observar en la vida cotidiana: carreteras, líneas telefónicas, líneas de televisión por cable, el transporte colectivo metro, circuitos eléctricos de nuestras casas, automóviles, etc, las cuales tienen su representación gráfica como sus recorridos y sus soluciones mediante grafos y árboles.
En el Capítulo VII se tiene autómatas de estado finito o máquinas de estado finito, es un modelo matemático de un sistema, herramienta muy útil para especificar aspectos relacionados con tiempo real, dominios reactivos o autónomos, computación reactiva, protocolos, circuitos y arquitecturas de software.
Finalmente en el Capítulo VIII se presenta el fundamento de Lenguajes formales y lenguajes naturales, en matemáticas, lógica, y ciencias de la computación, un lenguaje formal es un conjunto de palabras (cadenas de caracteres) de longitud finita formadas a partir de un alfabeto (conjunto de caracteres) finito.
En el Capítulo II presenta Álgebra de Boole que permite presentar funciones con dos estados.
En el Capítulo III se presenta Mapas de Karnaugh que permiten simplificar las funciones algebraicas.
En el Capítulo IV Se tiene las técnicas de conteo las variaciones, permutaciones y combinaciones las cuales son parte de las Matemáticas Discretas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
En el Capítulo V y en el Capítulo VI se presenta la teoría de grafos, árboles y sus aplicaciones, para nadie es novedad observar en la vida cotidiana: carreteras, líneas telefónicas, líneas de televisión por cable, el transporte colectivo metro, circuitos eléctricos de nuestras casas, automóviles, etc, las cuales tienen su representación gráfica como sus recorridos y sus soluciones mediante grafos y árboles.
En el Capítulo VII se tiene autómatas de estado finito o máquinas de estado finito, es un modelo matemático de un sistema, herramienta muy útil para especificar aspectos relacionados con tiempo real, dominios reactivos o autónomos, computación reactiva, protocolos, circuitos y arquitecturas de software.
Finalmente en el Capítulo VIII se presenta el fundamento de Lenguajes formales y lenguajes naturales, en matemáticas, lógica, y ciencias de la computación, un lenguaje formal es un conjunto de palabras (cadenas de caracteres) de longitud finita formadas a partir de un alfabeto (conjunto de caracteres) finito.
Exámenes Parciales, Finales y Ejercicios Resueltos de Matemática Discreta
SOFTWARE
Utilidades Matemáticas
Descargar
Arboles de Operaciones Binarias
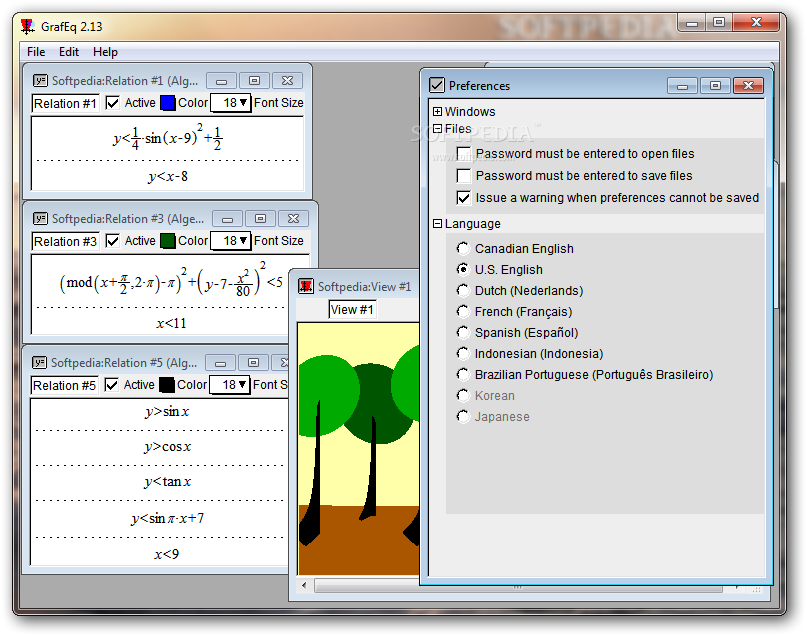
GrafEq es un software que permite representar gráficamente expresiones algebraicas y otras relaciones, pero que tiene como particularidad la posibilidad de obtener en forma automática el árbol de una expresión.
No es de uso libre, pero puede desacargarse una versión de evaluación, funcionalmente completa que no expira, salvo porque aparace cada 10 minutos un mensaje recordando que se trata de una versión no registrada.
Cada relación, expresión o función puede presentarse en GrafEq graph en tres formas:
- Simbólica - Una definición algebraica, que usa notación matemática usual, y presentada en una o más ventanas del "Álgebra" (Algebraic. Cada relación puede contener una o más restricciones, tales como ecuaciones, inecuaciones, definición de un conjunto o definición condicional). En esta ventana se ingresa la expresión.
- Estructural - un diagrama de flujo, o interpretación en árbol, presentada en una o más ventanas de "Estructura", en la que puede verse el árbol de la expresión.
- Gráfica - una representación cartesiana o polar, presentada en una o más ventanas de "Vista".
yEd Graph Editor






ya no sirven los link subelos de nuevo porfa
ResponderEliminarLink caidos xD
ResponderEliminarcarnal subelos opasamelos porfa ami me in
ResponderEliminarinteresa
pasamelos
jowel_50pumas@hotmail.com
se nota que no le das mantenimiento a tu pagina, que barbaro, desde noviembre te lo estan pidiendo, nooooooo que perdida de tiempo contigo en serio
ResponderEliminaramigo puedes volver a subir los libros o restaurar los links te agradecería mucho
ResponderEliminarPOrfavor subelos de nuevo
ResponderEliminarSube nuevos links!!!
ResponderEliminarLinks caídos, resubelos por favor
ResponderEliminarFortunately, it is not that difficult to find video SEO marketing service that's right for you. What search engines will the SEO service target with your campaign. The first service is based on registering a domain name and adding of local IP address in local languages in the targeted market.
ResponderEliminarmy page :: Référencement
En efec los links estan rotos imposible descargar
ResponderEliminarnoooooooooooo funcionaaaaaaaaaaaaaaaaaaaaa!!!!
ResponderEliminar